洛谷P2168 荷马史诗
洛谷P2168 荷马史诗
题目背景
追逐影子的人,自己就是影子 ——荷马
题目描述
Allison 最近迷上了文学。她喜欢在一个慵懒的午后,细细地品上一杯卡布奇诺,静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》 组成的鸿篇巨制《荷马史诗》实在是太长了,Allison 想通过一种编码方式使得它变得短一些。
一部《荷马史诗》中有 nn 种不同的单词,从 11 到 nn 进行编号。其中第 ii 种单词出现的总次数为 w_iw**i。Allison 想要用 kk 进制串 s_is**i 来替换第 ii 种单词,使得其满足如下要求:
对于任意的 1\leq i, j\leq n1≤i,j≤n ,i\ne ji=j ,都有:s_is**i 不是 s_js**j 的前缀。
现在 Allison 想要知道,如何选择 s_is**i,才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下,Allison 还想知道最长的 s_is**i 的最短长度是多少?
一个字符串被称为 kk 进制字符串,当且仅当它的每个字符是 00 到 k-1k−1 之间(包括 00 和 k-1k−1 )的整数。
字符串 str1str1 被称为字符串 str2str2 的前缀,当且仅当:存在 1 \leq t\leq m1≤t≤m ,使得 str1 = str2[1..t]str1=str2[1..t]。其中,mm 是字符串 str2str2 的长度,str2[1..t]str2[1..t] 表示 str2str2 的前 tt 个字符组成的字符串。
输入格式
输入的第 11 行包含 22 个正整数 n, kn,k ,中间用单个空格隔开,表示共有 nn 种单词,需要使用 kk 进制字符串进行替换。
接下来 nn 行,第 i + 1i+1 行包含 11 个非负整数w_iw**i ,表示第 ii 种单词的出现次数。
输出格式
输出包括 22 行。
第 11 行输出 11 个整数,为《荷马史诗》经过重新编码以后的最短长度。
第 22 行输出 11 个整数,为保证最短总长度的情况下,最长字符串 s_is**i 的最短长度。
输入输出样例
输入 #1复制
1 | 4 2 |
输出 #1复制
1 | 12 |
输入 #2复制
1 | 6 3 |
输出 #2复制
1 | 36 |
说明/提示
【样例解释】
样例 1 解释
用 X(k)X(k) 表示 XX 是以 kk 进制表示的字符串。
一种最优方案:令 00(2)00(2) 替换第 11 种单词, 01(2)01(2) 替换第 2 种单词, 10(2)10(2) 替换第 33 种单词,11(2)11(2) 替换第 44 种单词。在这种方案下,编码以后的最短长度为:
1 × 2 + 1 × 2 + 2 × 2 + 2 × 2 = 121×2+1×2+2×2+2×2=12
最长字符串 s_is**i 的长度为 22 。
一种非最优方案:令 000(2)000(2) 替换第 11 种单词,001(2)001(2) 替换第 22 种单词,01(2)01(2) 替换第 33 种单词,1(2)1(2) 替换第 44 种单词。在这种方案下,编码以后的最短长度为:
1 × 3 + 1 × 3 + 2 × 2 + 2 × 1 = 121×3+1×3+2×2+2×1=12
最长字符串 s_is**i 的长度为 33 。与最优方案相比,文章的长度相同,但是最长字符串的长度更长一些。
样例 2 解释
一种最优方案:令 000(3)000(3) 替换第 11 种单词,001(3)001(3) 替换第 22 种单词,01(3)01(3) 替换第 33 种单词, 02(3)02(3) 替换第 44 种单词, 1(3)1(3) 替换第 5 种单词, 2(3)2(3) 替换第 66 种单词。
【数据规模与约定】
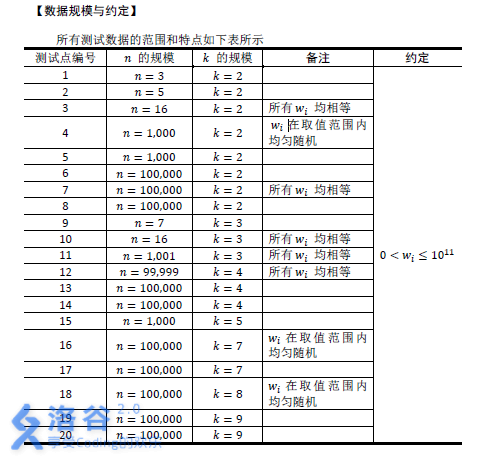
【提示】
选手请注意使用 64 位整数进行输入输出、存储和计算。



分析
纯纯的哈夫曼树,我竟然没写出来。
主要是没想明白不是二进制的哈夫曼怎么构造,也是看了题解才知道,其实是一样的。
如果不是2进制的哈夫曼树,可能会存在这种情况,就是每次弹出相应数量的节点后,最后一层,也就是最靠近根的一层会填不满,这样不就浪费了嘛,所以可以在开始的时候,就把缺少的节点构建成权值为0的节点(这样不会有影响),压入队列中就可以了。
到底缺少几个也不太好想,K进制,每次取出K个合成一个新的,再放回去,总的来说就是去掉了K - 1个,因为N个节点最后要生成1个节点,所以要去掉N - 1个,这样就可以判断了,如果(N - 1)%(K - 1)为0,就表示不用添加,否则就把这多出来的补成K - 1个,就是添加(k - 1)- (N - 1)%(k - 1)。
代码
1 |
|
洛谷P2168 荷马史诗

